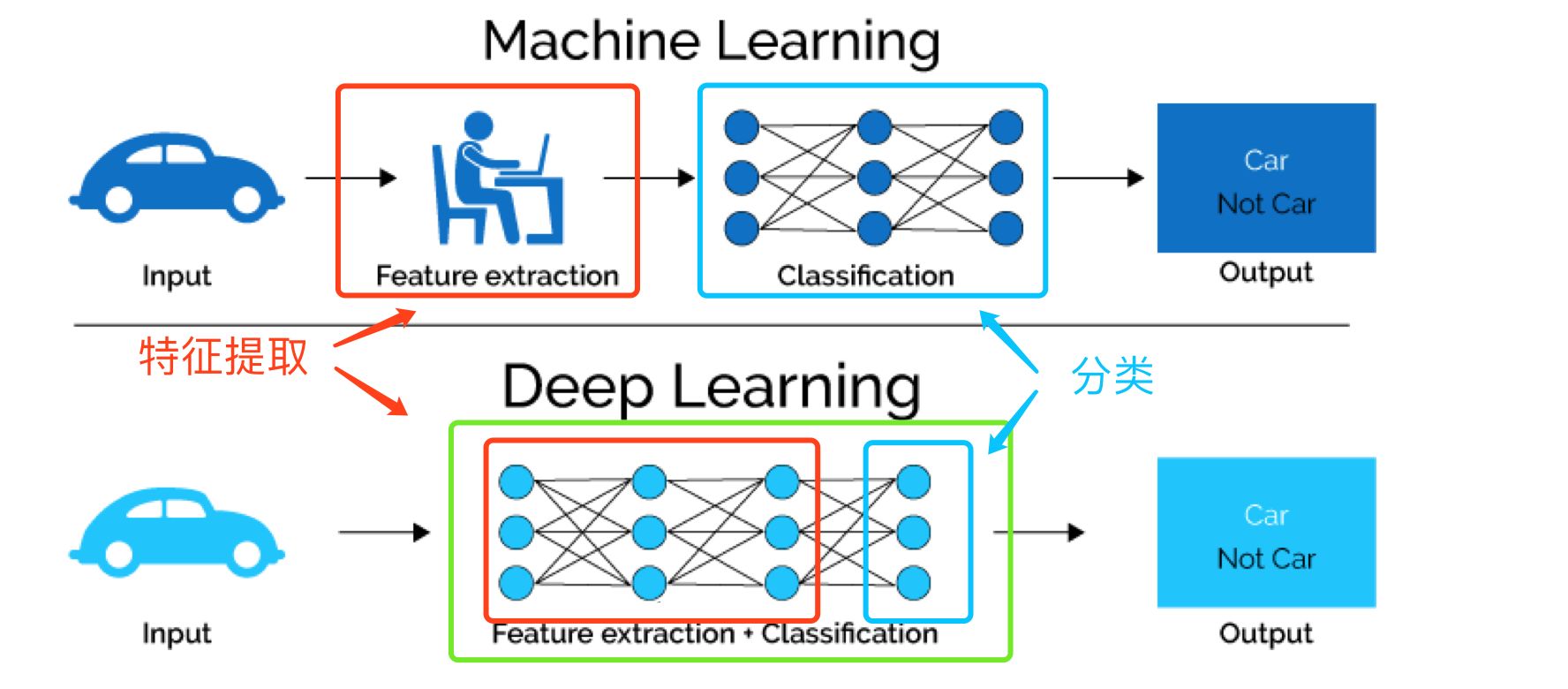
图神经网络(一)预备知识
图的基本概念
对一些接触过数据结构的朋友来说,图的概念并不陌生。**图(Graph)是由若干顶点(Vertex 或 Node)和连接这些顶点的边(Edge)构成的。**设一个图$G=(V,E)$,其中$V={v_1,v_2,\cdots,v_n}$表示$G$的顶点集,$E\subseteq V\times V$表示$G$的边集,则有如下概念:
邻接矩阵(Adjacent Matrix)
一种直接的存储图基本信息的方法就是使用邻接矩阵$\bold{A}^{n\times n}$。矩阵的边(一维数组)表示顶点集,用边张成的二维矩阵用来表示顶点之间的边的连接信息。若顶点$v_i$与$v_j$之间有边连接,则令邻接矩阵中对应的元素值$\bold{A}{ij}=1$,否则$\bold{A}{ij}=0$。当需要存储边的权重时,可令$\bold{A}_{ij}$为对应值。保存了权重值的邻接矩阵称为权重图(Weighted Graph)。
度(Degree)
一个顶点的度指的是与该顶点相连的边的数量。顶点的度数与边数存在数量关系$\sum_{v\in V}degree(v)=2|E|$。即顶点的度之和为边数的两倍。
度矩阵(Degree Matrix)
图$G$的度矩阵$D$是一个$n\times n$的对角阵,其对角线上的元素为对应顶点的度:$d_{ii}=degree(v_i)$。
路径(Path)
图的一条路径是由顶点和边交替构成(起点和终点均为顶点)的一个序列:$v_0,e_1,v_1,e_2,v_2,\cdots,e_k,v_k$。
距离(Distance)
若顶点$u$到顶点$v$的最短路径存在,则这条最短路径的长度称为$u,v$之间的距离。若它们之间没有路径,则距离为无穷大。
邻居节点(Neighborhood)
若顶点$v_i$和$v_j$之间有边相连,则$v_i$和$v_j$互为邻居节点。若其距离为$K$,则称$v_i$为$v_j$的$K$阶邻居节点。
简易图论
拉普拉斯矩阵
对一个顶点数为$n$的图$G$