Welcome to Ylxy's Blog

在本文中，我们将介绍如何使用Selenium Grid构建一个分布式爬虫。我们将从Selenium Grid的基本概念和架构开始，然后逐步深入到如何搭建分布式环境以及编写分布式爬虫代码。 Selenium Grid简介 Selenium Grid是什么？ Selenium Grid是一个用于分布式运行和管理Selenium WebDriver测试的开源工具。它允许在多个浏览器、操作系统和设备之间并行执行自动化测试，从而提高测试的效率和覆盖率。Selenium Grid的核心组件包括一个中心节点（Hub）和多个工作节点（Node）。这种架构使得开发者可以将测试任务分发到不同的节点上运行，以适应不同的环境需求。 通过使用Selenium Grid，我们可以： 快速地在不同浏览器、操作系统和设备上执行测试，加快开发周期。 提高测试覆盖率，确保Web应用程序在各种环境下的兼容性和稳定性。 并行执行测试用例，节省时间和计算资源。 Selenium Grid不仅适用于Web应用程序的功能测试和兼容性测试，还可以用于构建分布式爬虫，提高爬虫的爬取效率和稳定性。 为什么要使用Sele ...

何为GPU？ GPU是英文Graphics Processing Unit（图形处理器）的缩写，是一种专门设计用于高速处理图像、视频和其他图形数据的处理器。GPU最初是为了帮助计算机快速处理复杂的3D图形而设计的，但现在已广泛应用于许多其他领域，如机器学习、科学计算和图形处理等。 相比于CPU（中央处理器），GPU拥有更多的核心和更高的并行性能，使其能够更快地处理大规模的数据集。GPU还拥有更多的内存和更快的内存带宽，这对于一些需要大量内存和带宽的任务来说非常重要。在没有GPU的时候，人们想将计算机中的数据显示在屏幕上，是使用CPU来进行相关运算的。我们要做的事情简单概括一下，就是通过对数据进行相应的计算，把数据转换成一个又一个图片上的像素，然后将这张图片显示在屏幕上。整个流程中的计算并不复杂，但是数量大，且计算流程重复，如果全盘交给CPU的话会给其造成很大的性能负担。于是乎GPU诞生了： 下面我们来看看GPU与CPU的区别： 可以看到，GPU采用了数量众多的计算单元和超长的流水线，但只有非常简单的控制逻辑并省去了Cache。而CPU不仅被Cache占据了大量空间，而且还有有复杂的控 ...

图的基本概念 对一些接触过数据结构的朋友来说，图的概念并不陌生。**图（Graph）是由若干顶点（Vertex 或 Node）和连接这些顶点的边（Edge）构成的。**设一个图$G=(V,E)$，其中$V={v_1,v_2,\cdots,v_n}$表示$G$的顶点集，$E\subseteq V\times V$表示$G$的边集，则有如下概念： 邻接矩阵（Adjacent Matrix） 一种直接的存储图基本信息的方法就是使用邻接矩阵$\bold{A}^{n\times n}$。矩阵的边（一维数组）表示顶点集，用边张成的二维矩阵用来表示顶点之间的边的连接信息。若顶点$v_i$与$v_j$之间有边连接，则令邻接矩阵中对应的元素值$\bold{A}{ij}=1$，否则$\bold{A}{ij}=0$。当需要存储边的权重时，可令$\bold{A}_{ij}$为对应值。保存了权重值的邻接矩阵称为权重图（Weighted Graph）。 度（Degree） 一个顶点的度指的是与该顶点相连的边的数量。顶点的度数与边数存在数量关系$\sum_{v\in V}degree(v)=2|E|$。即顶点的度之 ...

极大似然估计的定义 相关定义 极大似然估计（MLE）是建立在极大似然原理的基础上的一种参数估计的方法。所谓极大似然原理，通俗理解就是，一个事件发生的原因就是该事件发生的概率较大。假设在一个随机试验中有若干结果事件$A、B、\dots$，若$A$出现，则可以认为该试验对$A$的出现有利，即该试验中$A$出现的概率较大。例如，设甲箱中有99个白球，1个黑球；乙箱中有1个白球。99个黑球。现随机取出一箱，再从抽取的一箱中随机取出一球，结果是黑球，则这一黑球从乙箱抽取的概率比从甲箱抽取的概率大得多，这时我们自然更多地相信这个黑球是取自乙箱的。 一般来说，事件$A$发生的概率与未知参数$\theta$有关，其发生的概率为$P(A|\theta)$。若在一次试验中$A$发生了，MLE则要求我们应该选择使$P(A|\theta)$达到最大的参数$\theta$。在详细介绍MLE之前，先让我们来了解一下何为参数化模型。参数化模型就是用有限个参数来表示概率密度函数集$\mathrm{q}(\boldsymbol{x} ; \boldsymbol{\theta})$。其中$\boldsymbol{x}$为 ...

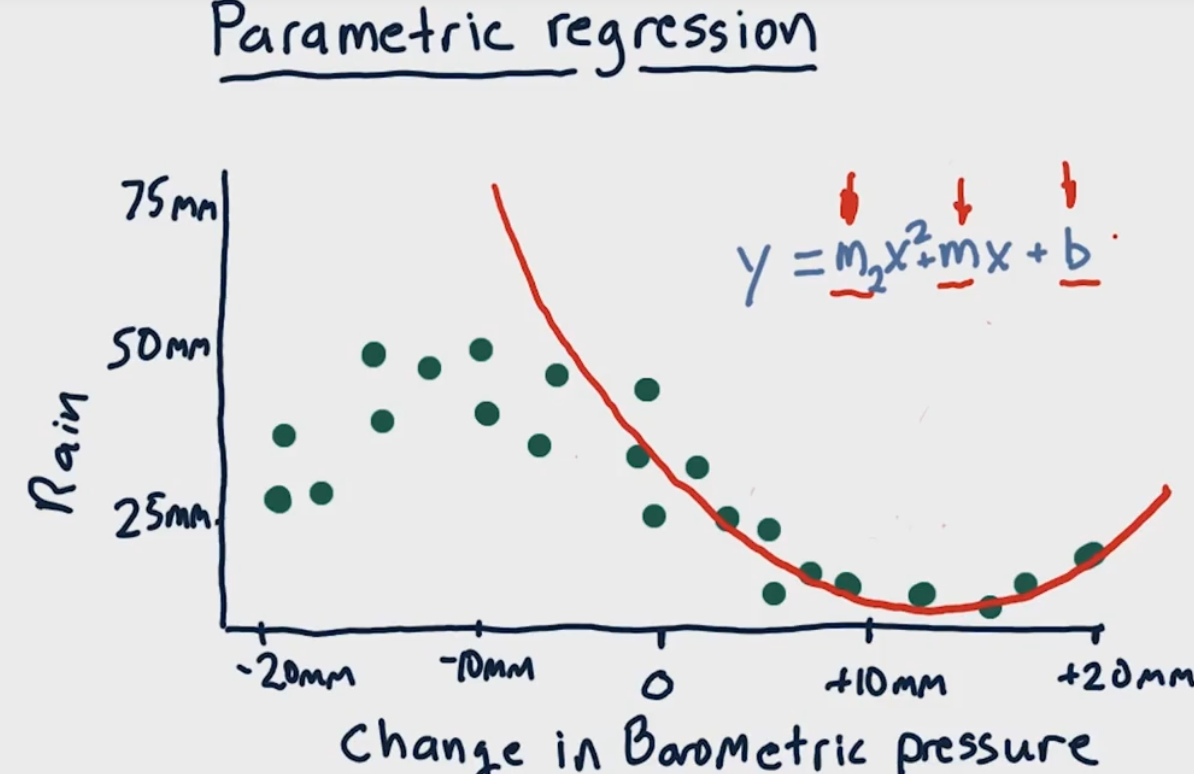
线性回归模型 日常生活中，我们往往会碰到连续特征的预测问题。例如房价预测，股价预测等。这种类型的问题统称“回归”问题。解决这类问题的学习方法是有监督的。设有一个数据集$D$，其特征$\mathbf{x}$的维度为$d$，输出为$y$，$y$是连续型的。则回归问题致力于寻找一个函数$f$以建立$\mathbf{x}$到$y$的映射$y=f(\mathbf{x})$。 常见的回归模型分为==线性模型==和==非线性模型==两种。其中线性模型形式简单，易于建模。非线性模型可在线性模型的基础上通过引入层级结构或高维映射得到。本小节我们先讨论线性模型。 基本形式 设输入数据$\mathbf{x}=(x_1,x_2,\cdots,x_d)$，则线性模型是通过将输入数据的属性进行线性组合来得到的模型： $$ f(\boldsymbol{x})=w_{1} x_{1}+w_{2} x_{2}+\ldots+w_{d} x_{d}+b $$ 我们也可以用向量表示： $$ f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b $ ...

当我们在conda中创建新的虚拟环境后，别忘了将新建的虚拟环境添加进Jupyter notebook内核，否则每次启动Jupyter notebook都会进入默认的base环境下导致新安装的包无法使用。具体操作步骤如下：（本文新建的虚拟环境以py37为例） 进入新建的虚拟环境 1conda activate py37 安装nb_conda 1conda install nb_conda 安装ipykernel 1conda install -n py37 ipykernel 将虚拟环境写入Jupyter notebook 1python -m ipykernel install --user --name py37 --display-name "显示名称" 此处注意--display-name后接的是在jupyter notebook中显示的虚拟环境名称（可以自定义），不要忘记双引号。 执行完之后，就能在jupyter notebook中看到新建的虚拟环境了：） 1

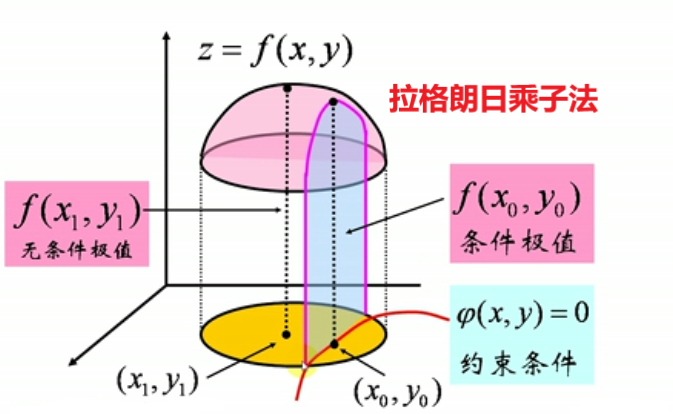
在我们的实际生活中，优化问题通常包括三类：无约束优化问题，等式约束优化问题以及不等式约束优化问题。其中无约束问题求解最为简单，直接求导验证即可。而带有约束条件的问题则比较棘手，往往不能通过简单的消元法求解。这时，我们可以通过构造$Lagrange$函数，将约束问题的目标函数和约束条件加以结合。此时，问题简化为无约束问题，我们就能通过求解$Lagrange$函数的优化问题来得到原约束问题的近似解。 算法框架 构造对应的$Lagrange$函数 求解变量的偏导方程 将结果代入目标函数 下面我们对等式约束问题和不等式约束问题分别进行讨论。 等式约束问题的乘子法 考虑如下等式约束问题： $$ \min f(x),\ \ \\\text{s.t. }h_i(x)=0, \ \ (i\in E={1,\cdots,m_1}) $$ 定义如下函数$\tilde{L}_\mu{(x)}$ $$ \tilde{L}_\mu(x)=L(x,\lambda^*)+\frac{1}{2}\mu S(x) $$ 其中， $$ L(x, \lambda)=f(x)-\sum_{i \in E} \lambda ...

关于测试程序我暂时没有在网上找到一份能够完美运行的教程，遂记录一下我运行成功的案例。 当我们搭建好一个htcondor的pool并且能够通过condor_status看 到节点资源的时候，我们可以通过如下来运行一些测试job： 提交一个简单的condor任务 下面我们提交一个判断1~100素数的例子： 按如下层级结构创建文件夹： job/ # 任务主文件夹 job/error/ # 存放报错信息 job/input/ # 存放输入文件 job/log/ # 存放日志文件 job/output/ # 存放stdout文件 在job下新建一个可执行程序prime.sh 当我们使用cat > 文件名编辑内容时建议从其他地方直接复制，编辑完毕后按ctrl+D退出。 123456789101112131415161718192021222324root@ylxy2:/home/ylxy2/job# cat > prime.sh#!/bin/bash# Determine if argument is a p ...